17 Лекций по общей и прикладной ценологии

(применительно к электричеству)

 

Лекция 7. Моделирование Н-распределений простыми числами

и пойнтер-точка R

 

Существенные отличия рассматриваемых трёх форм Н-распределения от закона Парето–Ципфа не снимает вопроса об общности структуры физико-химических, биологических, технических (технетических), информационных, социальных ценозов. Фундаментальность явления, определяемого отбором – конкурентной борьбой за ресурс (как показал Трубников Б. А.), описывается математической моделью распределения такой, что её можно поставить в ряд (вывести по аналогии) с распределениями Ферми–Дирака и Бозе–Эйнштейна.

Но есть ещё одно фундаментальное свойство, демонстрируемое на видовом (и ранговидовом) Н-распределении. Оно заключается в возможности соотнести понятие вид простому числу, где бы оно ни находилось как сомножитель в факториале натурального числа. Фундаментальность (если встать на точку зрения, восходящую к Пифагору и Платону) заключается в том, что числа правят миром, что Вселенная и сама жизнь устроены так, что есть некоторые идеальные образы, которым соответствуют числа или их комбинации.

Примем, как уже указывалось в предыдущей лекции, в качестве канонического дискретное распределение простых сомножителей в факториале некоторого числа N. Факториал – функция, определённая на множестве целых неотрицательных чисел, значение которой равно произведению натуральных чисел от 1 до натурального числа n, т. е. 1·2·3…·n; обозначается n! (по определению, 0!=1). Факториал равен числу перестановок из n элементов. При больших n приближённое выражение факториала определяется формулой Стирлинга в асимптотике:

n!≈n·nn·e-n,        n®∞   .                                                                      (1)

Простое число – натуральное (целое положительное) число р>1, имеющее только два делителя – 1 и р:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43,                                              (2)

Числа, имеющие не менее трёх различных делителей, называются составными.

Элементарная теория чисел утверждает, что всякое натуральное число, отличное от единицы – либо простое, либо, если оно составное, может быть представлено в виде произведения простых чисел. При этом такое представление единственно (с точностью до расположения сомножителей). Запись этого произведения в виде степеней одинаковых простых чисел, а самих простых чисел – в порядке возрастания, даёт каноническое разложение натурального числа

Ni=·    mj≥0 (j=0, 1, 2, …, m),                                               (3)

где mj – степень (встречаемость) простого числа (как штуки-особи); q1 – простое число как вид из ряда (2); r – ранг простого числа (его номер по порядку), последний номер – число видов – самих простых чисел в системе S.

Простые числа играют роль очень своеобразных "кирпичиков", из которых строятся все остальные натуральные числа. Евклид в 3 веке до н. э. доказал бесконечность множества простых чисел; Эратосфен – способ их отсеивания из множества натуральных чисел; Эйлер нашёл доказательство бесконечности множества простых чисел. Чебышев вывел неравенство, которому должно удовлетворять количество π(х) простых чисел р≤х:

a<π(х)<b.                                                                                      (4)

Обратимся к задаче определения (в постановке Эйлера) очередного простого числа, большего известного произвольного натурального числа х по известным простым числам, меньшим х. Эйлер ввёл функционал

n(x)≈x/lnx   ,                                                                                               (5)

где π – функция, равная количеству простых чисел, меньших х.

Свяжем (3), (5) с терминологией видового и ранговидового Н-распределения. Тогда х равен натуральному числу N, а его факториал используется вместо произвольного числа, так как существует ряд предельных теорем, связывающих число N с особями – простыми сомножителями, а само N задаёт все виды – простые числа (показатели mj определяют наибольший общий делитель двух натуральных чисел). Ряд (2) может быть продолжен: 137, 139, 149, 151, …, 509, 521, 623, 541, …, 40001, …, (2756839–1), …. Изучение простых сомножителей в N! осуществлено нами вплоть до 100000!. Для построения шкалы объёмов выборок была использована экспоненциальная форма представления факториала, которую затем дважды логарифмировали:

N!=1010;                    N1=log(log строятся все остальные натуральные числа. Евклид в 3 веке до н. э. доказал бесконечность множества простых чисел; Эратосфен – способ их отсеивания из множества натуральных чисел; Эйлер нашёл доказательство бесконечности множества простых чисел. Чебышев вывел неравенство, которому должно удовлетворять количество π(х) простых чисел р≤х:

a<π(х)<b.                                                                                       (4)

Обратимся к задаче определения (в постановке Эйлера) очередного простого числа, большего известного произвольного натурального числа х по известным простым числам, меньшим х. Эйлер ввёл функционал

n(x)≈x/lnx   ,                                                                                               (5)

где π – функция, равная количеству простых чисел, меньших х.

Свяжем (3), (5) с терминологией видового и ранговидового Н-распределения). Тогда х равен натуральному числу N, а его факториал используется вместо произвольного числа, так как существует ряд предельных теорем, связывающих число N с особями – простыми сомножителями, а само N задаёт все виды – простые числа (показатели mj определяют наибольший общий делитель двух натуральных чисел). Ряд (2) может быть продолжен: 137, 139, 149, 151, …, 509, 521, 623, 541, …, 40001, …, (2756839–1), …. Изучение простых сомножителей в N! осуществлено нами вплоть до 100000!. Для построения шкалы объёмов выборок была использована экспоненциальная форма представления факториала, которую затем дважды логарифмировали:

N!=1010;                    N1=log(logN!),                                                      (6)

придя к результатам, качественно не отличающимся от результатов, полученных для 101! или 1021!

Всего было рассмотрено три модели:

1) ранг r=1 присваивается всем простым числам, встретившимся в N! ровно один раз; ранг r=2 – объединению чисел, состоящих из двух сомножителей (4, 6, 9, 10, 14, 15, …); затем r=3 – из трёх (8, 12, 16, 18, 24, … и т. д.);

2) каждому простому числу – ранг по порядку; количество видов приравнивается сумме рангов; количество особей – произведению номера ранга на количество данных простых сомножителей;

3) представленная выражением (3).

Приемлемого физического истолкования для первых двух моделей найти не удалось, поэтому в исследовании, например, количества установленных и ремонтируемых двигателей как основная принята модель (3), в которой m – степень (встречаемость) простого числа, r – ранг простого числа. Например, N20=20 состоит из сомножителей N20=q12q20q31=2·2·5, где вид q1 (двойка) встретился как особь два раза, вид q3 (пятёрка) – один раз (q2 – тройка). В целом (табл. 1) для факториала, например, Ni=1021! двойка (саранчёвый вид) q1=2 встретилась (как особь) m1=1013 раз, тройка – 508 раз (q2=3, m2=508) и т. д. Согласно табл. 2 по одному разу (ноева каста) встретилось 75 простых чисел. Последний номер r=i (для Ni=1021! r=172) определяет число видов в системе S!), (6) придя к результатам, качественно не отличающимся от результатов, полученных для 101! или 1021!

Всего было рассмотрено три модели:

1) ранг r=1 присваивается всем простым числам, встретившимся в N! ровно один раз; ранг r=2 – объединению чисел, состоящих из двух сомножителей (4, 6, 9, 10, 14, 15, …); затем r=3 – из трёх (8, 12, 16, 18, 24, … и т. д.);

2) каждому простому числу – ранг по порядку; количество видов приравнивается сумме рангов; количество особей – произведению номера ранга на количество данных простых сомножителей;

3) представленная выражением (3).

Приемлемого физического истолкования для первых двух моделей найти не удалось, поэтому в исследовании, например, количества установленных и ремонтируемых двигателей как основная принята модель (3), в которой m – степень (встречаемость) простого числа, r – ранг простого числа. Например, N20=20 состоит из сомножителей N20=q12q20q31=2·2·5, где вид q1 (двойка) встретился как особь два раза, вид q3 (пятёрка) – один раз (q2 – тройка). В целом (табл. 1) для факториала, например, Ni=1021! двойка (саранчёвый вид) q1=2 встретилась (как особь) m1=1013 раз, тройка – 508 раз (q2=3, m2=508) и т. д. Согласно табл. 2 по одному разу (ноева каста) встретилось 75 простых чисел. Последний номер r=i (для Ni=1021! r=172) определяет число видов в системе S. Cумма чисел 75+58+42+…+508+1013 (сумма особей всех видов) определяет число особей ценоза (длина текста).

Количество каст К=32 есть число заполненных строчек. Оценка численности первой касты производится с использованием теоремы о простых числах W1=N/2lnN. Остальные значения ряда можно получить аналитически, однако проще и точнее (из-за дискретности величин) получать их прямым счётом. Ранговое представление сомножителей простых чисел как модель ценозов можно применять в абсолютных числах как ряд, аналогичный, например Ni=1023! (отметим всплеск для 1024!, где прибавляются только двойки – их десять), если известно значение S (или U), или как относительную частоту (в табл. 2 и 1 приведены видовое и ранговидовое распределения).

 

Таблица 1. Ранговидовое Н-распределение         Таблица 2. Видовое H –распределение

 

i

m

pi

i

m

pi

i

M

pi

i

m

pi

 

К

i

W(i)

iW(i)

1

1013

2

44

5

193

87

2

449

130

1

733

1

1

75

75

2

508

3

45

5

197

88

2

457

131

1

739

2

2

29

58

3

253

5

46

5

199

89

2

461

132

1

743

3

3

14

42

4

168

7

47

4

211

90

2

463

133

1

751

4

4

8

32

5

101

11

48

4

223

91

2

467

134

1

757

5

5

7

35

6

84

13

49

4

227

92

2

479

135

1

761

6

Б

5

30

7

63

17

50

4

229

93

2

487

136

1

769

7

7

3

21

8

55

19

51

4

233

94

2

491

137

1

773

8

8

1

8

9

45

23

52

4

239

95

2

499

138

1

787

9

9

4

36

10

36

29

53

4

241

96

2

503

139

1

797

10

10

2

20

11

34

31

54

4

251

97

2

509

140

1

809

11

11

1

11

12

27

27

55

3

257

98

1

521

141

1

811

12

12

2

24

13

24

41

56

3

263

99

1

523

142

1

821

13

14

2

28

14

23

43

57

3

269

100

1

541

143

1

823

14

15

1

15

15

21

47

58

3

271

101

1

547

144

1

827

15

16

1

16

16

19

53

59

3

277

102

1

557

145

1

829

16

17

1

17

17

17

59

60

3

281

103

1

563

146

1

839

17

19

1

19

18

16

61

61

3

283

104

1

569

147

1

853

18

21

1

21

19

15

67

62

3

293

105

1

571

148

1

857

19

23

1

23

20

14

71

63

3

307

106

1

577

149

1

859

20

24

1

24

21

14

73

64

3

311

107

1

587

150

1

863

21

27

1

27

22

12

79

65

3

313

108

1

593

151

1

877

22

34

1

34

23

12

83

66

3

317

109

1

599

152

1

881

23

36

1

36

24

11

89

67

3

331

110

1

601

153

1

883

24

45

1

45

25

10

97

68

3

337

111

1

607

154

1

887

25

55

1

55

26

10

101

69

2

347

112

1

613

155

1

907

26

63

1

63

27

9

103

70

2

349

113

1

617

156

1

911

27

84

1

84

28

9

107

71

2

353

114

1

619

157

1

919

28

101

1

101

29

9

109

72

2

359

115

1

631

158

1

929

29

168

1

168

30

9

113

73

2

367

116

1

641

159

1

937

30

253

1

253

31

8

127

74

2

373

117

1

643

160

1

941

31

508

1

508

32

7

131

75

2

379

118

1

647

161

1

947

32

1013

1

1013

33

7

137

76

2

383

119

1

653

162

1

953

32

2614

172

2942

34

7

139

77

2

389

120

1

659

163

1

967

 

 

В табл. 1: i – ранг вида, начиная с наибольшей популяции; m – числен-ность вида; pi – наимено-вание вида (простого числа). В табл. 2: К –  номер касты (группы); i – числен-ность особей каждого из W(i) видов; W(i) – количество видов в касте; iW(i) – число особей в касте.

 

 

35

6

149

78

2

397

121

1

661

164

1

971

 

 

36

б

151

79

2

401

122

1

673

165

1

977

 

37

б

157

80

2

409

123

1

677

166

1

983

 

38

6

163

81

2

419

124

1

683

167

1

991

 

39

б

167

82

2

421

125

1

691

168

1

997

 

40

5

173

83

2

431

126

1

701

169

1

1009

 

41

5

179

84

2

433

127

1

709

170

1

1013

 

42

5

181

85

2

439

128

1

719

171

1

1019

 

43

5

191

86

2

443

129

1

727

172

1

1021

 

Нумерация каст в видовом распределении имеет физический смысл: это номера по прядку всех существующих популяций. Ошибки (экспериментальные) для редких видов перемещают вид из касты в соседнюю (также малочисленную), ошибки в определении числа особей для многочисленных видов, как правило, даже не меняют номер касты (при их сплошной нумерации). Это даёт однозначное распределение каст, канонизированное в виде ряда простых чисел, т. е. при заданном S все остальные параметры получаются строго однозначно (например, N0 – число двоек – есть численность саранчёвой касты К=32; при ранговом распределении – численность первого ранга).

Возвратимся к Н-моделированию, в котором видовое распределение представлено в виде

Ω(х)=W0/x1+α,                                                                                              (7)

а ранговидовое как

Λ(r)=B/rβ.                                                                                                   (8)

Представим хвост гиперболы (7) от пойнтер-точки R  (см. предыдущую лекцию) далее в виде рис. 1. Очевидно модельное представление реально существующего – прямой (физически объяснимой: меньше единицы нет области существования). Объяснение же этого Н-распределением в виде спадающей кривой (уходящей в область, меньшую единицы) – уж слишком грубое приближение. Естественны для модели простых чисел провалы и выбросы. Сравните (табл. 2) отношения W(i) каст 1 и 2, 2 и 3, 4 и 5, всплеск для К=9. Заметьте, что своеобразие отношений каст 28–32 рассчитываемо: троек в N! меньше чем двоек, пятёрок – чем троек и т. д.

 

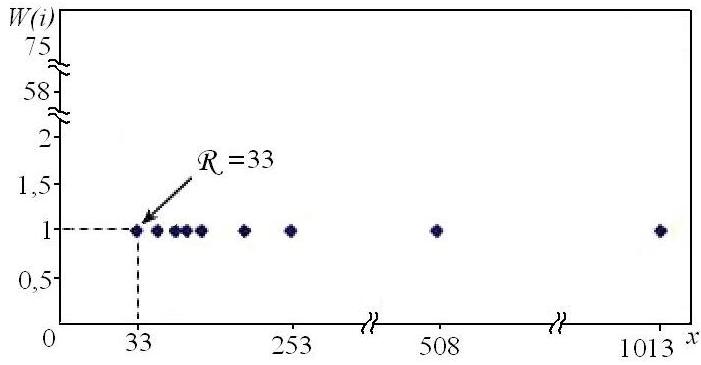
Рис. 1. Представление "хвоста гиперболы" применительно

к распределению сомножителей простых чисел (см. табл. 1 и 2)

 

Поэтому возникает возможность использования точки R, определяемой (когда Ω(х)≡1) для всей области существования х[1, ¥):

Θ(х)=                                                                                            (9)

где ρ определяется из выражения W1/S=ρ/i1+ρ.

Возвратимся ещё раз к рисунку, где пойнтер-точка близка к 33, но фактически отсутствует (см. табл. 2). После R по одному разу встретилось как вид 1013 двоек-особей; тройки как вид – 508 раз; пятёрки – 253; семёрки – 168, далее – простые числа-виды (по табл. 1) 168, 101, 84, 63¸55, 45, 36, 34. Очевидно, что "хвост" можно представить в виде ранговидового распределения: r1=1013; r2=508; r3=253; … и описать его формулой Λ(r)=B/rβ.

В качестве обобщения подхода предложим табл. 3, в которой n – число, факториал которого рассматривается как n=N; S – общее количество простых чисел; W(1) – фактическая, а W0 – теоретическая, по Ципфу, первая точка; виды, встретившиеся ровно один раз (ноева каста); U – количество особей для факториала S!; N(1) – численность наибольшей популяции (саранчёвая каста – количество двоек); k – количество каст; α – характеристический показатель. Полезно заметить, что N(1)≈n, и именно здесь возможны всплески "саранчи" – двоек, троек, пятёрок. Важно, что всплеск не бывает одновременно для нескольких видов.

Модель простых чисел даёт существенное отличие от представлений Хольцмарка, Лотки, Брэдфорда, Виллиса, Фишера, Ципфа, Мандельброта: для заданного количества видов существует единственный ряд, однозначно определяющий гиперболическое Н-распределение и его параметры. Может быть предложена теорема, подобная теореме Вейерштрасса.

 

Таблица 3. Обобщающие характеристики Н-распределения канонического разложения

Число n

S

U

W(1)

N(1)

k

ρ·10-3

α·10-3

W0

U/S

101

26

240

11

97

11

793

301

22

9,2

401

79

1086

33

397

21

780

372

40

13,7

901

154

2578

67

896

31

823

422

129

16,7

1601

252

4728

113

1597

39

858

457

212

18,8

2501

367

7551

163

2495

47

847

466

309

20,6

3601

503

11054

225

3596

57

855

481

424

22,0

4901

654

15247

291

4895

63

849

487

551

23,3

6401

834

20127

382

6397

70

883

506

705

24,1

8101

1019

25705

461

8092

82

868

508

862

25,2

10001

1229

31987

560

9995

87

877

516

1040

26,0

12101

1448

38970

659

12093

97

875

520

1226

26,9

14401

1687

46666

768

14396

105

876

542

1430

27,7

16901

1949

55070

862

16897

113

882

530

1654

28,3

19601

2223

64177

1015

19595

121

879

533

1887

28,9

22501

2516

74008

1157

22491

128

888

593

2138

29,4

25601

2819

84556

1293

25597

140

885

541

2396

30,0

28901

3146

95818

1451

28893

144

892

546

2677

30,5

32401

3477

107805

1594

32392

154

884

546

2958

31,0

36101

3834

120515

1765

36095

160

889

550

3266

31,4

40001

4203

133947

1941

39995

167

892

553

3580

31,9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При разложении каждого числа Ni натурального ряда на простые сомножители существует алгоритм преобразования факториала NS, где S – номер наибольшего простого числа в факториале такой, что начиная с некоторого произвольного числа исключением отдельных видов можно получить ряд, идентичный опытным (экспериментальным) гиперболическим Н-рядам с поправкой, связанной с изменением числа сомножителей, равных их числу между NS-1 и NS+1. Тогда возникает возможность сравнить два экспериментальных (статистических) ряда, полученных в любой из наук не по характеристическому показателю, числу видов и особей, а по каждому наблюдению (восстановление ряда программно). Тем самым как-будто моделируется эволюция: осуществляется отбор уничтожением каких-либо видов.

Это ключевое утверждение проявлется в следующем: 1) видовое Н-распределение является тем объектом познания, который соответствует процессу и результату физики структурирования – каждый элемент (особь как вид) начинает существование с ноевой касты, содержательно отражающей эволюционное новое и фиксирующей отмирание;

2) i=[х] есть не ранг, а величина численности популяции тех видов, каждый из которых представлен одинаковым количеством штук-особей и которые, формально поэтому образуют касты, множество которых объективно образует ценоз;

3) видовое разнообразие ценоза математически до точки R описывается гиперболическим Н-распределением (7) таким, что α>0 существенно неразличимо для i=k, где i=1, 2, 3, …; k=1, 2, 3, …, К, а начиная с некоторого k становится i≠k, где i>k;

4) разность i–k до точки R равна сумме видов после точки на оси х Ω(х)≡1, которая из-за дискретности особей, образуемых из факториала ряда (2), и прерывности гиперболы (7) в общем случае не совпадает с R (может быть не целой), тем самым порождая ошибку; 5) немногочисленные виды после R (5–10 % от общего объёма словаря V; для 1021! по табл. 2 это 6,4 %) суммарным количеством штук-особей составляют основную структурную массу ценоза*, по Шрейдеру это 40–60 % объёма текста, по табл. 2 – 80,3 %.

Обратим внимание ещё на возможность свёртки в ограниченное количество шагов (экспериментальный материал не содержит больше четырёх таких шагов). По существу, видовое распределение есть свёртка ранговидового (см. табл. 1): 75 единиц (от i=98 до i=172) объединено в одну касту (см. табл. 2) и т. д. Можно сделать следующий шаг: свернуть видовое распределение. Но многократная свёртка невозможна.

При рассмотрении общности законов построения ценозов и исследовании разнообразия и соотношения "крупное-мелкое", как правило, нечётко формулируется возможность переноса результатов из одной области знаний в другую. Изучение технических ценозов имеет преимущества в строгости перед биоценозами и в динамике – перед математической лингвистикой (вообще перед областью информационных и социальных исследований): во-первых, относительно устоявшиеся представления о системе показателей и структуре цеха, производства, завода; города, региона, государства; во-вторых, наличие бухгалтерской, в идеале, статистики; в-третьих, возможность отследить эволюцию вида, опускаясь до отдельной особи (большинство технических видов родилось на наших глазах). Типы техноэволюции и биоэволюции – не сопоставимы, но взаимное моделирование многообещающе.

Реальное существование и эволюция ценозов могут быть описаны системой показателей-параметров, которые не обязательно представимы числом. Впрочем, и за числом зачастую видятся качественные отличия, например, объём доменной печи или памяти компьютера.

Говоря о связях между видами (особями) одного ценоза, ещё раз обратим внимание на единичность связи типа "хищник–жертва" Вольтерра. Хотелось бы предложить модель значимых связей отдельных особей всех видов ценозов, основанную на качественной оценке её адекватности. Пусть задан натуральный ряд чисел. Для достаточно большого значения числа, казалось бы, разложение на простые сомножители (виды) должно давать "длинные" произведения. Но это оказалось не так. Возьмём часть ряда от одного простого числа до другого (см. ниже):

 

220333

простое число

220334

2·41·2687

220335

3·5·37·397

220336

2·2·2·2·47·293

220337

13·17·997

220338

2·3·3·12241

220339

7·31477

220340

2·2·5·23·479

220341

3·11·11·607

220342

2·29·29·131

220343

19·11597

220344

2·2·2·3·9181

220345

5·127·347

220346

2·7·15739

220347

3·3·3·8161

220348

2·2·31·1777

220349

179·1231

220350

2·3·5·5·13·113

220351

простое число

 

Среднее число связей, включая одно из простых чисел, составляет 3,7. Любопытно! (гипотеза "короткости" связей проверена для техноценозов, хотя лишь дважды). Заметим, что отношение объёма текста Т≡U к объёму словаря V≡S для "Евгения Онегина" оказалось равным d=4,51; для двигателей Карметкомбината d=12,56. Конечно, есть саранчёвые всплески 2n, 3m, …, но они лишь подтверждают ценологические свойства натурального ряда.

Если для описания множества электродвигателей (единиц электропривода или иных электроприёмников) с целью выделения таких групп, которые корреляционно связаны (в частности режимом работы), применима гипотеза об использовании модели простых чисел, то это открывает новые пути для изучения электрического хозяйства (объектов электрики) и обеспечивает практичность модели. Тогда возникает необходимость более широкого рассмотрения разных сочетаний сомножителей каждого из чисел натурального ряда. Выполним идентификацию взаимосвязей между элементами ценоза (табл. 3), представив числовые образы в пространстве простых чисел.

Ограничимся рядом 2, 3, 4, …, 31, 32 (столбец 1). Каждое число ряда разложим на простые сомножители (ст. 2). Назовём ансамблем каждое из множеств табл. 3, составленное концептуально и состоящее из элементов, характеризующих ансамбль. Если сосчитать количество простых сомножителей для каждого из случаев ряда 2, …, 32, то очевидно, что ансамблей (чисел ряда) 31, а общее число сомножителей как элементов – 65 (ст. 2). Если взять собственно простое число (ст. 10), то каждое из них образует ансамбль, не имеющий связей и состоящий из одного элемента (11 из 11, ст. 7). Сомножители-особи некоторых составных чисел одинаковы (одного вида). Тогда ансамбль (их семь) есть одновидовые числа (ст. 4), а элемент – сомножитель ансамбля (их 21).

 

Таблица 4. Простые сомножители и их связи в числах

Число

ряда

Простые

сомно-

жители

Их

число

Связи

Ранг про-

стого числа

Всего

сомно-

жителей

Простое

число

внутри вида

между видами

смешан-ные

нет связи

1

2

3

4

5

6

7

8

9

10

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

2

3

2×2

5

2×3

7

2×2×2

3×3

2×5

11

2×2×3

13

2×7

3×5

2×2×2×2

17

2×3×3

19

2×2×5

3×7

2×11

23

2×2×2×3

5×5

2×13

3×3×3

2×2×7

29

2×3×5

31

2×2×2×2×2

1

1

2

1

2

1

3

2

2

1

3

1

2

2

4

1

3

1

3

2

2

1

4

2

2

3

3

1

3

1

5

 

 

2

 

 

 

3

2

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

2

 

3

 

 

 

 

5

 

 

 

 

2

 

 

 

2

 

 

 

2

2

 

 

 

 

 

2

2

 

 

 

2

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

3

 

3

 

 

 

4

 

 

 

3

 

 

 

 

1

1

 

1

 

1

 

 

 

1

 

1

 

 

 

1

 

1

 

 

 

1

 

 

 

 

 

1

 

1

 

1

2

 

3

 

4

 

 

 

5

 

6

 

 

 

7

 

8

 

 

 

9

 

 

 

 

 

10

 

11

 

31

14

 

7

 

4

 

 

 

2

 

2

 

 

 

1

 

1

 

 

 

1

 

 

 

 

 

1

 

1

2

3

 

5

 

7

 

 

 

11

 

13

 

 

 

17

 

19

 

 

 

23

 

 

 

 

 

29

 

31

Всего: ансамблей

элементов

31

65

7

21

8

17

5

16

11

11

 

 

65

 

 

Можно выделить межвидовые связи (столбец 5) такие, что в ансамбль входят только числа, где нет сомножителей одного вида (таких 8: это числа 6, 10, 14, 15, 21, 26, 30, в которые вошли 17 сомножителей-элементов). Смешанными связями названы ансамбли (их пять), каждый из которых включает повторяющиеся и иные виды (ст. 6). Проранжировав простое число (ст. 8), определим их общее количество (S=11, это и есть объём словаря V), сосчитав двойки, тройки и т. д. (ст. 9) и просуммировав их, получим 65 – общее количество сомножителей в факториале 32! как тексте. Данные представленной табл. 4 есть лишь заявка на исследования, а сама гипотеза связей станет доказанной только в результате статистических наблюдений.

Современный глобализующийся эволюционизм и требования постиндустриального информационного общества поменяли производство, науку и искусство, повседневную жизнь. Принятие решения в этих условиях требует понимания, что первая классическая научная картина мира описывает часть бытия; вторая – вероятно-статистическая, опирающаяся на вторую постнеклассическую картину, описывает большее число фактов. Предлагаемая ценологическая модель простых чисел служит одним из математических описаний постнеклассического ценологического мировоззрения третьей научной картины мира.

 

Контрольные вопросы

1.     Определите простое число, его факториал и подсчитайте число сомножителей для отрезка ряда от 31 до 50.

2.     Поясните каноническое разложение натурального числа

3.     Проанализируйте видовое Н-распределение и укажите на особенности пойнтер-точки R.

4.     Прокомментируйте ранговидовое Н-распределение и поясните соотношение m для начала табл. 1

5.     Поясните ключевое утверждение, касающееся особенностей видового Н-распределения табл. 2.

6.     Оцените совпадение с реальностью связей между видами для части ряда между двумя простыми числами.

7.     Продолжите до 50 число ряда табл. 4 и выскажите свои гипотезы об особенностях столбцов табл. 4.


* Это соответствует распространившимся утверждениям: 20 % мужиков выпивают 80 % пива; или: 90 % диссертантов не "двигают" науку, а создают лишь фон. Отметим, что из 10 %, получивших новое и сделавших ощутимый шаг в науке, лишь один из миллиона делает эпохальный шаг.