//
Электрификация металлургических предприятий Сибири. Вып.12. – Томск: Изд-во Том. ун-та, 2005. С. 291–300.
НЕГАУССОВОСТЬ СОЦИАЛЬНЫХ ЯВЛЕНИЙ И ЭВОЛЮЦИЯ
Хайтун С.Д.
Стационарные (не содержащие
времени) распределения значений социальных переменных являются в своей массе
негауссовыми, т. е. не могут быть описаны распределением Гаусса и другими
гауссовыми распределениями, подчиняющимися центральной предельной теореме и
закону больших чисел теории вероятностей. Негауссовость распределения
проявляется в том, что при больших значениях переменной оно имеет распределения
Ципфа[1]
![]() (1)
(1)
с небольшим значением показателя
этого распределения α, негауссовость генеральной совокупности – в
росте моментов распределения с объемом выборки. В логарифмических координатах
распределение Ципфа имеет вид прямой линии, по углу наклона которой к осям
координат может определяться графически показатель α.
Обнаружив
около четверти века назад феномен негауссовости социальных явлений [1–3][2], автор этих строк
утверждал, что эволюция в сторону возрастания энтропии связана с переходом от гауссовых распределений, доминирующих в природных
системах, к негауссовым, преобладающим в системах социальных,
что органический мир занимает в этом ряду промежуточное положение и что социальный
мир эволюционирует в сторону все более творческих видов человеческой
деятельности как более негауссовых.
Сегодня
я готов подписаться подо всем сказанным ранее относительно социального мира,
однако в отношении неорганического и органического миров должен внести существенные
коррективы. В статье [8] нами уже были высказаны сомнения относительно правомерности
жесткого противопоставления природных систем как гауссовых социальным как
негауссовым. Здесь мы более решительно откажемся от такой дихотомии, вписав негауссовые
распределения в представления об универсальной эволюции, в рамках которых в
едином ключе рассматривается эволюция всего сущего – от Большого взрыва до био- и ноосферы на Земле.
Разумеется, я с самого начала знал по
литературе (и писал), что в неорганическом и органическом мирах встречаются
распределения Ципфа – анионов и катионов по встречаемости в морской воде[3],
химических элементов по встречаемости в земной коре и в нашей Метагалактике[4],
космических тел по массе [11, 12], космических же частиц по энергии и т. д., –
но сегодня становится ясно, что негауссовые распределения встречаются в природе гораздо чаще, чем это думалось ранее.
Во-первых, негауссовыми
оказываются распределения, описывающие распределения особей данного вида по поверхности
Земли[5].
Негауссовы и распределения растительных видов в лесу по биомассе (кривые
доминирования разнообразия)[6].
Более того, выяснилось, что поведение
животных характеризуется распределениями, негауссовость которых не уступает
негауссовости человека. Построенные нами распределения,
характеризующие поведение муравьев, оказались распределениями Ципфа со
значениями ![]() [7],
тогда как, скажем, распределение ученых по числу публикаций описывается
распределением Ципфа с
[7],
тогда как, скажем, распределение ученых по числу публикаций описывается
распределением Ципфа с ![]() [2. С. 258],
а распределение слов научного сленга в §§ 6 и 9 первой статьи Эйнштейна по
специальной теории относительности – распределением Ципфа с
[2. С. 258],
а распределение слов научного сленга в §§ 6 и 9 первой статьи Эйнштейна по
специальной теории относительности – распределением Ципфа с ![]() [2. С.
275].
[2. С.
275].
Тот факт, что мозг животных,
включая насекомых, генерирует распределения, сравнимые по степени негауссовости
с человеческими, впечатляет. Но это только
подтверждает то, что, по-видимому, негауссовые распределения в социальной и
органической сферах генерируются нейронными структурами человека и животного,
точнее – отдельными нейронами, которые у человека и муравья функционируют
практически одинаково.
Во-вторых, сегодня все яснее
становится, что распространенность негауссовых распределений тесно связана с фрактальностью
наблюдаемого мира. Негауссовость является
общим свойством пространственных и непространственных[8]
фрактальных (точнее, фракталоподобных[9])
структур. В случае пространственных фракталов речь идет о негауссовости
распределений фрактальных (под)систем по размерам и
расстояниям между ними[10], в
случае непространственных фракталов негауссово распределены составляющие фракталы
(под)системы по значениям непространственных величин, характеризующих
(под)системы и "барьеры" между ними[11].
Поскольку же фракталы и на самом деле чрезвычайно распространены в наблюдаемом
мире, постольку чрезвычайно распространены в нем и негауссовые распределения.
Фракталоподобная
структура наблюдаемого мира, на наш взгляд, является следствием эволюционного
принципа минимакса [19], обеспечивая на каждый текущий момент времени
максимальное разнообразие типов разноуровневых структур и отвечающих им форм
взаимодействий, что дает, в свою очередь, максимальную интенсивность процессов
превращения друг в друга разных форм взаимодействий. Вот это разнообразие типов
возникающих во фракталах структур и описывается негауссовыми распределениями.
Поскольку интенсивность метаболизмов в ходе эволюции нарастает, постольку
вектор эволюции направлен одновременно и в сторону все большей негауссовости
наблюдаемых явлений.
Если стóит чему-то удивляться, так это тому, что в наблюдаемом
мире, наряду с негауссовыми, достаточно часто встречаются и гауссовые
распределения, особенно в окружающей нас на Земле природной среде. Гауссовы, к
примеру, распределения особей по весу, размерам и значениям многих других параметров.
Похоже на то, что это во многом объясняется гравитацией, которая существенно
ограничивает размеры земных объектов. В общем случае ширина распределений, т. е.
степень их негауссовости, определяется не только гравитацией, но и другими
взаимодействиями. Там, где эти внешние ограничения несущественны, распределение
объектов оказывается негауссовым, как негауссово, например, упоминавшееся
распределение космических тел по массе.
Не являясь
мерой беспорядка для реальной системы
[15. Гл.
9], энтропия является таковой в случае отдельно взятого распределения: чем оно шире и,
следовательно, проще по форме, тем больше его энтропия. Распределения, имеющие бóльшую энтропию, более длиннохвосты, т. е.
более негауссовы, отвечая
большему разнообразию форм. Таким образом, эволюция в сторону все большей
негауссовости явлений означает эволюцию в сторону распределений со все большей энтропией. Точнее говоря, речь может идти о
том, что в ходе эволюции растет доля распределений с такой максимально
большой энтропией. Другими словами, с ходом эволюции все более негауссовыми
становятся генеральные
совокупности распределений.
Похоже, в частности, на то, что в органическом мире удельный вес ментальных
факторов ниже, чем в социальном. Я по-прежнему полагаю, что если
бы для органического мира была построена случайная выборка стационарных распределений
и для каждого из них было найдено значение параметра a негауссового
распределения, то "органическое" распределение значений a
оказалось бы менее негауссовым, чем построенное нами распределение для социального
мира с ![]() [1. С. 128], т.е. имело бы большее значение a. В более широком плане, если
бы для всех распределений наблюдаемого мира можно было построить распределение
значений характеризующего эти распределения показателя распределения Ципфа a, то
с ходом эволюции это распределение становилось бы все более негауссовым, т.е.
характеризовалось бы все бóльшим значением энтропии и все меньшим значением
a..
[1. С. 128], т.е. имело бы большее значение a. В более широком плане, если
бы для всех распределений наблюдаемого мира можно было построить распределение
значений характеризующего эти распределения показателя распределения Ципфа a, то
с ходом эволюции это распределение становилось бы все более негауссовым, т.е.
характеризовалось бы все бóльшим значением энтропии и все меньшим значением
a..
Бóльшая негауссовость
социальных явлений по сравнению с органическими и неорганическими
подтверждается большей вероятностностью первых по
сравнению со вторыми и третьими. Негауссовые распределения существенно шире гауссовых. Именно поэтому в социальных дисциплинах
относительно редка ситуация, столь частая в естественных науках, когда вследствие
узости распределения оно может быть охарактеризовано одним лишь средним значением
переменной и когда вероятностный подход вырождается в
детерминистический. По этой же причине в естественных науках
зависимости между переменными определяются независимо от распределений значений
этих переменных (имеет место примат зависимостей над распределениями), тогда
как в социальной сфере непосредственное определение зависимостей между переменными
оказывается неэффективным (имеет место примат распределений над зависимостями)
[1. С. 20–28].
[1] Распределение, переходящее
при больших значениях переменной в распределение Ципфа, мы называем ципфовым.
Ципфовое распределение, не являющееся распределением Ципфа, отклоняется от него
в области малых значений переменной. Во многих случаях это отклонение является
артефактом, будучи следствием процедуры формирования
выборки. К примеру, распределение жителей данного города по
их научному вкладу, измеряемому с использованием открытой шкалы [1. С.
80–83], скорее всего окажется распределением Ципфа,
поскольку бóльшая часть жителей, как и требует это распределение, имеет
нулевой научный вклад. Такое же распределение для живущих в том же городе
ученых, оставаясь ципфовым, распределением Ципфа уже не будет, поскольку ученый
по определению имеет ненулевой научный вклад. Во втором случае распределение
строилось по значениям той же переменной, по значениям которой
"обрезалась" выборка при её формировании. Напротив, в первом случае
выборка, как мы говорим, является чистой относительно измеряемой
переменной. Нами была выдвинута гипотеза, согласно которой
для отдельного индивида и чистой выборки стационарное распределение всегда
имеет форму распределения Ципфа [1. С. 133–142; 2.
С. 185–186, 197]. В любом случае использование только
чистых выборок приведет к существенному увеличению доли распределений Ципфа
среди негауссовых распределений.
2
О большой распространенности распределения Ципфа в мире техники см. [4–6], в
археологии – [7]. Мы же говорим о распространенности не столько распределения Ципфа, сколько ципфовых распределений, что сообщает
нашему наблюдению бóльшую общность, поскольку в социальной сфере
встречается много ципфовых распределений, не являющихся распределением Ципфа.
3
Использовав данные, содержащиеся в книге Ю.Одума [9. С. 286], мы построили ранговое распределение 5 анионов по
количеству на ![]() ) и такое же распределение для 4 катионов (оно имеет вид распределения
Ципфа с
) и такое же распределение для 4 катионов (оно имеет вид распределения
Ципфа с ![]() ).
).
4 Воспользовавшись
таблицей, приведенной в книге К.Фолсома [10. С. 16],
мы построили ранговое распределение 15 химических элементов по их
распространенности в нашей Метагалактике. Получилось ципфовое
распределение с a»1,18.
5 Мы построили 4 таких распределения по табличным данным, приведенным
Ю.Одумом [9]: (1) ранговое распределение 8 квадратов поверхности Земли площадью
![]() ), (2) ранговое распределение 4 квадратов поверхности Земли
площадью
), (2) ранговое распределение 4 квадратов поверхности Земли
площадью ![]() ), (3) ранговое распределение 6 квадратов поверхности Земли
площадью
), (3) ранговое распределение 6 квадратов поверхности Земли
площадью ![]() ), (4) ранговое распределение 22 видов птиц по их
представленности в сосновом лесу (ципфовое распределение с
), (4) ранговое распределение 22 видов птиц по их
представленности в сосновом лесу (ципфовое распределение с
![]() ).
).
6 Ю.Одум [9.
С. 132] приводит такие распределения для четырех типов лесов.
7 Три примера таких распределений: (1) ранговое
распределение разных элементов поведения (прерывистый бег, ориентирование с обследованием
возвышенностей, подробное обследование небольших участков почвы и т.д.) у
муравья Formica pratensis по процентной доле времени
для поведенческого ансамбля "окологнездовые выходы" (![]() ); (2) то же для поведенческого ансамбля
«фуражирование» (
); (2) то же для поведенческого ансамбля
«фуражирование» (![]() ) (3) ранговое распределение трех видов муравьев – Formica cumicilaria, Lasius alienus и Formica pratensis – по уровню исследовательской
активности, определяемой по отношению времени, затрачиваемого муравьями на обследование
моделей (подземный лабиринт, щетка, параллельные пластины) реальных природных
ситуаций (подземных ходов, расщелин между камнями, толщи травостоя), ко времени,
расходуемому на пребывание на открытой поверхности арены (
) (3) ранговое распределение трех видов муравьев – Formica cumicilaria, Lasius alienus и Formica pratensis – по уровню исследовательской
активности, определяемой по отношению времени, затрачиваемого муравьями на обследование
моделей (подземный лабиринт, щетка, параллельные пластины) реальных природных
ситуаций (подземных ходов, расщелин между камнями, толщи травостоя), ко времени,
расходуемому на пребывание на открытой поверхности арены (![]() ). Распределения построены по табличным
данным, приведенным Ж.И.Резниковой [13. С. 60–61, 70].
). Распределения построены по табличным
данным, приведенным Ж.И.Резниковой [13. С. 60–61, 70].
8
И пространственные, и непространственные фракталы размещены в пространстве,
различаясь природой «барьеров», разделяющих фрактальные подструктуры и которые
во втором случае являются непространственными. Такими непространственными
«барьерами» разной проницаемости, разделяющими казалось бы
непрерывно переходящие друг в друга системы на дискретные (фрактальные)
структуры, служат, например, клеточные и субклеточные мембраны, клановые,
этнические и государственные границы. Пространственные фракталы чаще встречаются
в неорганическом мире, в котором нередко бывает применимо пространственное
(механическое) описание, для органического же и социального миров более
характерны непространственные фракталы. Определяющие свойства фракталов – системная иерархичность и мутовочность – сохраняются и в случае
непространственных фракталов.
9 Реальные
системы, размещенные в нашем трехмерном пространстве, из-за их конечности, не
могут быть «настоящими» фракталами (т. е. фракталами в математически строгом
смысле), поскольку в этом случае они имели бы нулевую меру, т. е. суммарный
объем, занимаемый их точками, был бы равен нулю, а с ним была бы равна нулю и
их масса. Поэтому реальные системы, за исключением
всей бесконечной Вселенной [14], могут быть только фракталоподобными, т. е.
проявлять фрактальность только в некотором конечном диапазоне масштабов [15.
С. 197–198].
10 Продемонстрируем генерирование негауссовых
распределений пространственными фракталами. Определение
фрактальной размерности [16. P. 43]
![]() или
или ![]() (С.1)
(С.1)
(![]() – число измерительных
«кубиков» размерности D и длиной грани e каждый, которыми
покрывается данное фрактальное множество при определении его меры) для числа n(x) подструктур с линейным размером
x дает выражение
– число измерительных
«кубиков» размерности D и длиной грани e каждый, которыми
покрывается данное фрактальное множество при определении его меры) для числа n(x) подструктур с линейным размером
x дает выражение
![]() ~
~![]() , (С.2)
, (С.2)
(мы отождествили M(e) с n(x) и e c x),
имеющее форму распределения Ципфа (1) с ![]() . Чем меньше a, т.е. D,
тем более негауссово данное распределение. Поскольку
собственная размерность D
фрактала, размещенного в нашем трехмерном пространства, меньше 3 (так как
фрактальная размерность фрактала меньше его топологической размерности, равной
размерности пространства, в котором он размещен [15. С.
61–62]), постольку показатель a генерируемых этими фракталами распределений Ципфа
меньше 2, а сами эти распределения существенно негауссовы. О
генерировании фракталами распределения Ципфа говорят, к примеру, и авторы работ
[17, 18].
. Чем меньше a, т.е. D,
тем более негауссово данное распределение. Поскольку
собственная размерность D
фрактала, размещенного в нашем трехмерном пространства, меньше 3 (так как
фрактальная размерность фрактала меньше его топологической размерности, равной
размерности пространства, в котором он размещен [15. С.
61–62]), постольку показатель a генерируемых этими фракталами распределений Ципфа
меньше 2, а сами эти распределения существенно негауссовы. О
генерировании фракталами распределения Ципфа говорят, к примеру, и авторы работ
[17, 18].
11 Примером непространственной фрактальной
(фракталоподобной) структуры, генерирующей негауссовые распределения, является
нейронная сеть мозга.
ПРИЛОЖЕНИЕ
Максимально правдоподобная
оценка a для распределения Ципфа
(1) с
![]() (П.1)
(П.1)
(при получении этого
выражения суммирование приближенно заменено интегрированием) дается уравнением
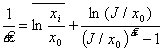 , где
, где
![]() . (П.2)
. (П.2)
В пренебрежении
зависимостью от J:
![]() . (П.3)
. (П.3)
Максимально
правдоподобная оценка a распределена асимптотически нормально на множестве
выборок фиксированного объема N из данной
генеральной совокупности с дисперсией [20. С. 547]:
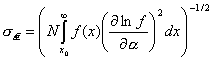 (П.4)
(П.4)
(в правой части a считается равным значению a0 на
генеральной совокупности). Приближенно записывая распределение Ципфа в виде
![]() (П.5)
(П.5)
(J и N полагаются
большими), получаем
![]() . (П.6)
. (П.6)
К сожалению, замена
суммирования на интегрирование при получении выражения (П.1) для параметра C приводит к катастрофе: оценка (П.2) оказывается
существенно завышенной. Положение однако не
безнадежно. Замена (П.1) на
![]() , (П.7)
, (П.7)
где
![]() , (П.8)
, (П.8)
приводит к корректному
уравнению для максимально правдоподобной оценки a: [21]
![]() . (П.9)
. (П.9)
Присутствие в нем
специальной функции ![]() и ее производной по a
и ее производной по a
![]() (П.10)
(П.10)
требует написания относительно
несложной математической программы, после чего определение выборочных значений a, мне кажется, станет рутинной операцией.
Все это верно лишь для частотной
формы распределения Ципфа. Что касается ранговой формы, то здесь еще и конь не
валялся. Между тем на негауссовых генеральных совокупностях чаще употребляется
именно она. В самом деле, частотная
форма распределения удобна (применима), когда выборочная относительная частота n(x)/N
служит статистически достоверной оценкой плотности вероятности f(x)
значения переменной x, т. е. когда мала относительная среднеквадратическая
ошибка ![]() относительной частоты n(x)/N:
относительной частоты n(x)/N:
![]() . (П.11)
. (П.11)
Это
имеет место, когда
![]() , (П.12)
, (П.12)
т. е.
когда
![]() <<
<<![]() , (П.13)
, (П.13)
где Dx – величина классовых интервалов, на которые
разделен размах J–x0 значений случайной величины x на
данной выборке[12].
Ранговая
форма удобна (применима), когда с достаточной статистической достоверностью
определяются значения случайной величины x, т.е. когда
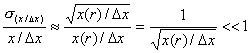 , (П.14)
, (П.14)
где Dx – снова классовый интервал. Условие (П.14) дает[13]
![]() >>
>>![]() . (П.15)
. (П.15)
Условия
(П.13) и (П.15) существенно различны. Частотная форма
тем применимее, чем больше объем выборки N и чем меньше J.
Ранговая форма применима практически при любом объеме выборки и тем применимее,
чем больше J.
В
естественных науках часто объемы выборок велики. Поэтому частотная форма здесь
удобна. Максимальные значения J переменной x здесь часто невелики
(стационарные распределения в естественных науках часто имеют короткие хвосты).
Поэтому ранговая форма здесь часто бывает неудобной. В социальных науках,
напротив, объемы выборок часто невелики, так что частотная форма здесь бывает
неудобной. J здесь, напротив, как правило, велико (поскольку
стационарные социальные распределения, как правило, имеют длинные хвосты). Поэтому
ранговая форма здесь часто удобна.
Соотношение
(П.15) дает простой рецепт повышения статистической достоверности результатов
при работе с ранговыми распределениями: следует уменьшать Dx, что связано с увеличением точности измерения
значений случайной величины x. Это заменяет увеличение объема выборки,
полезное в случае частотных распределений.
Заключаем, что сегодня оптимально
графическое определение показателя α.
Литература
1.
Хайтун С.Д.
Проблемы количественного анализа науки. М.: Наука, 1989. 280 с.
2.
Хайтун С.Д.
Наукометрия: Состояние и перспективы. М.: Наука, 1983. 344 с.
3.
4. Кудрин Б.И.
Введение в технетику. Томск: Изд-во ТГУ, 1993. 557 с.
5. Гнатюк В.И.
Оптимальное построение техноценозов. Теория и практика. Вып. 9. "Ценологические
исследования". М.: Центр систем. исслед., 1999. 272 с.
6. Фуфаев В.В.
Ценологическое определение параметров электропотребления, надежности, монтажа и
ремонта электрооборудования предприятий региона. М.: Центр систем исслед.,
2000. 320 с.
7. Ковалевская В.Б. Археологическая культура – практика, теория, компьютер. М.: Ин-т археологии
РАН, РФФИ, 1995. 193 с.
8. Хайтун С.Д.
Феномен негауссовости социальных явлений и эволюция // Техническая реальность в
XXI веке. Вып. 8. "Ценологические исследования".
М.: Центр системных исследований, 1999. С. 158-168.
9. Одум Ю.
Экология. Т. 2. М.: Мир, 1986. 376 с.
10. Фолсом К.
Происхождение жизни: Маленький теплый водоем. М.: Мир, 1982. 158 с.
11. Трубников Б.А.
Закон распределения конкурентов // Природа. 1993. № 11. С. 3–13.
12. Трубников Б.А.
О законе распределения конкурентов // Там же. 1995.
№ 11. С. 48–50.
13.
Резникова Ж.И. Межвидовые отношения муравьев. Новосибирск: Наука,
1983. 206
с.
14. Хайтун С.Д.
Эволюция Вселенной // Вопросы философии. 2004. № 10.
С. 74–92.
15. Хайтун С.Д.
Механика и необратимость. М.: Янус, 1996. 448 с.
16. Mandelbrot B.B. Fractals: Form,
Change, and Dimension.
17. Тимашев С.Ф.
Проявления макрофлуктаций в динамике нелинейных систем // Журн. физич. химии.
1995. Т. 69, № 8. С. 1349.
18. Малинецкий Г.Г., Потапов
А.Б.
Нелинейность. Новые проблемы, новые возможности // Новое
в синергетике. Загадки мира неравновесных структур. М.: Наука, 1996. С.
165–190.
19. Хайтун С.Д. Фундаментальная сущность
эволюции // Вопросы философии. 2001. № 2. С. 152–166.
20. Крамер Г.
Математические основы статистики. М.: ИЛ, 1948. 632 с.
21.
Ravichandra Rao J.K.
The distribution of scientific productivity and social change // J. Amer. Soc.
Inform. Sci. 1980. Vol. 31. P. 111–122.